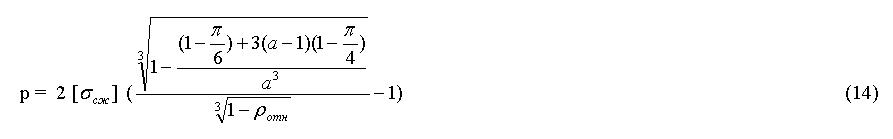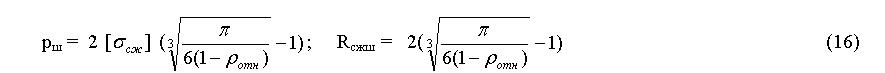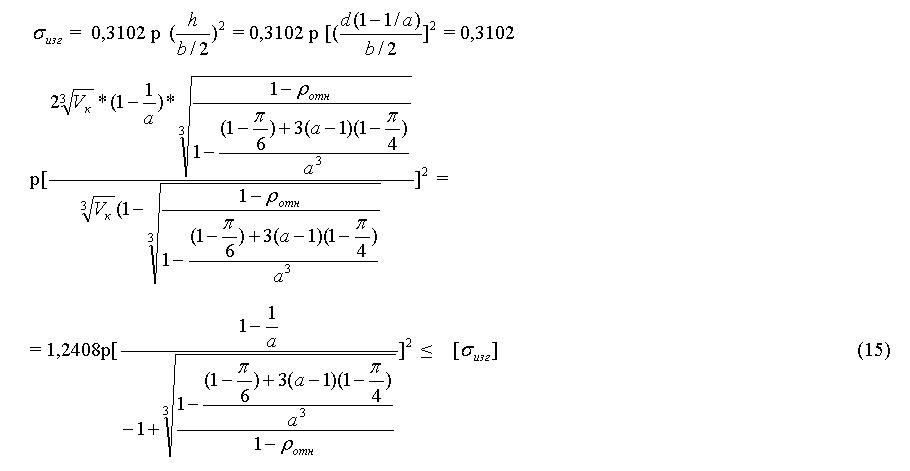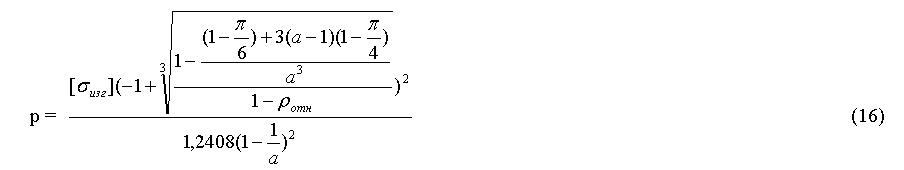Статьи
Н.А.Сапелин, А.Н. Сапелин. Влияние структуры пустот на прочность теплоизоляционных силикитных материалов
Интенсивное развитие и внедрение пористых теплоизоляционных силикатных материалов требует дальнейшего их исследования с целью создания технологии и оборудования по получению рациональной ячеистой структуры.
Одной из важнейших свойств теплоизоляционных силикатных материалов является прочность.
В 1963 году В.А. Пискнер получил теоретическую зависимость прочности ячеистого бетона от объемной массы[1].Он исходил из того, что шаровые пустоты расположены гексогонально и равномерно. Применив решение безмоментной теории для шарового купола при вертикальной нагрузке В.А.Пискнер получил следующую зависимость относительной прочности Ro ячеистого бетона от относительной плотности ρо:

где: Ro – относительная прочность ячеистого бетона (отношение прочности ячеистого бетона к прочности матрицы ячеистого бетона)
ρо - относительная плотность ячеистого бетона (отношение плотности ячеистого бетона к плотности матрицы ячеистого бетона)
На основании гипотезы о том, что прочность гипсового камня пропорциональна удельному числу контактов кристаллов двугидрата сульфата кальция друг с другом выведена теоретическая зависимость относительной прочности Ro гипсовых изделий от их относительной плотности ρо [2]:

Анализ данных зависимостей показывает, что они не учитывают структуру пустот.
Целью данной работы является теоретическое и экспериментальное обоснование влияния геометрических параметров пустот на прочность теплоизоляционных силикатных материалов (пористая керамика, пустотные гипсовые изделия, пенобетон и др.).
При рассмотрении зависимости прочности от структуры материала будем использовать допущения [3](стр.10÷12):
- материал тела за пределами поры имеет сплошное (непрерывное) строение
- материал тела за пределами поры изотропен, т.е. обладает во всех направлениях одинаковыми свойствами
- в теле до приложения нагрузки нет внутренних (начальных) усилий.
- весь материал [4] состоит из кубических ячеек размером
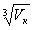 , где Vк – объем кубической ячейки. В каждой ячейке имеется пустота с определяющим размером d.
, где Vк – объем кубической ячейки. В каждой ячейке имеется пустота с определяющим размером d.
Пустоты могут быть различной формы: шаровые, эллипсоидные и другие.
Минимальная толщина перегородки в ячейке составляет
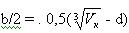
Рассмотрим кубическую ячейку размером 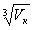 с пустотой определяющего размера d (Рис.1)
с пустотой определяющего размера d (Рис.1)
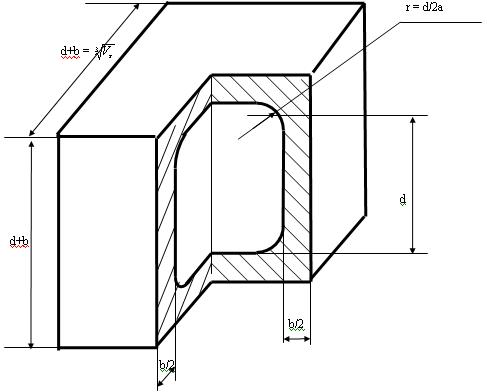
Рис.1. Кубическая ячейка пористого материала
Объем пустоты
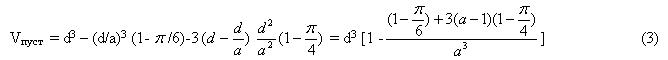
где а ≥ 1 – коэффициент, определяющий радиус скругления r = d/2a
При a = 1 r = d/2 - пустота имеет форму шара
Коэффициент К1[4], показывающий долю объема занимаемого пустотой в ячейке с определяющим размером d составит:
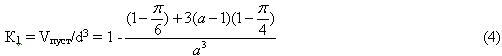
При а = 1 К1 =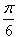
В нашем случае форма пустоты меняется значением коэффициента «а» (радиусом скругления r = d/2a). На рис.2 представлены различные формы пустоты в зависимости от коэффициента структуры «а».
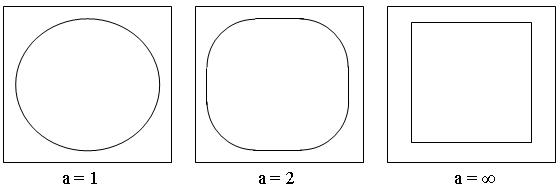
Рис.2. Зависимость формы пустоты от коэффициента структуры «а».
Из формулы (3) получаем:
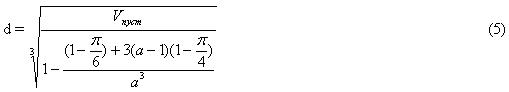
Задаемся относительной плотностью кубической ячейки
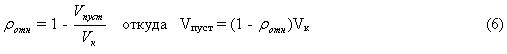
И тогда
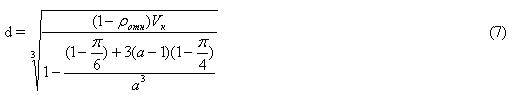
Толщина перегородки
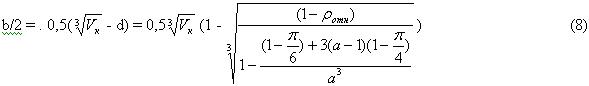
При шаровой форме пустоты (при а = 1)
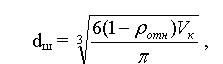
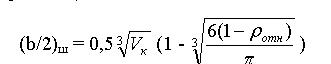 (9)
(9)
Рассмотрим верхнюю половину кубической ячейки с шаровой формой пустоты, нагруженную равномерной распределенной нагрузкой «р»
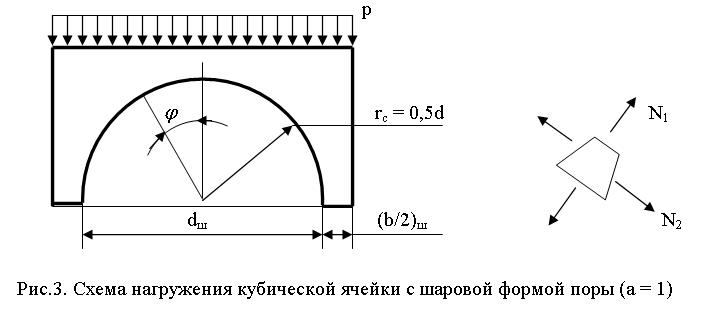
Для расчета возникающих усилий и напряжений воспользуемся безмоментной теорией расчета, применяемой при расчете куполов [5].
Усилие по направлению меридиана на единицу длины кольцевого сечения (N1 = ) [5].
N1 = - 0,5 р rс = - 0,25 рd, Н/м (10)
Кольцевое усилие на единицу длины меридиана (N2 = ) [5].
N2 = - 0,5 р rсCos2 = - 0,25 рd Cos2 , Н/м (11)
При Cos2 = 1 ( = 0) N2 = - 0,25 рd
Таким образом, максимальное усилие на единицу длины N1 = N2 = - 0,25 рd возникает при = 0 в точке с наименьшей толщиной перегородки (знак минус указывает, что возникают сжимающие усилия)
Максимальное напряжение сжатия при шаровой форме пустот

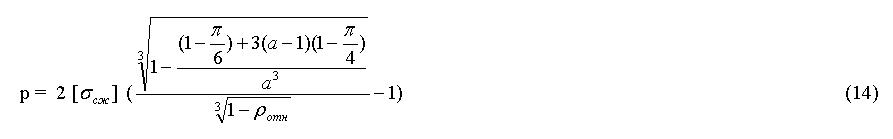
Относительная прочность (по отношению к сплошному материалу)

При шаровой форме пустоты
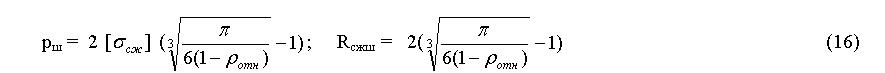
Рассмотрим кубическую ячейку материала с пустотой не шаровой формы (а ≥ 1)
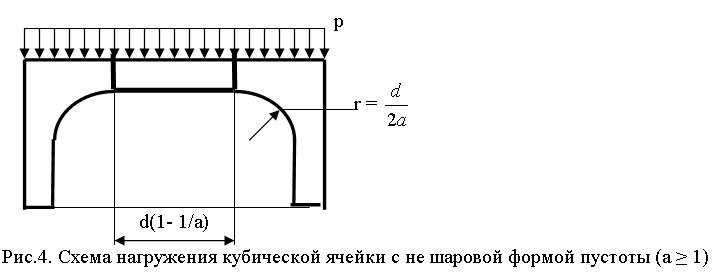
Т.к. в данном случае в середине кубической ячейки появляется участок с постоянной толщиной, то безмоментная теория не подходит. Поэтому рассмотрим участок с постоянной толщиной и применим метод расчета пластин, защемленных по контуру [6], [7].
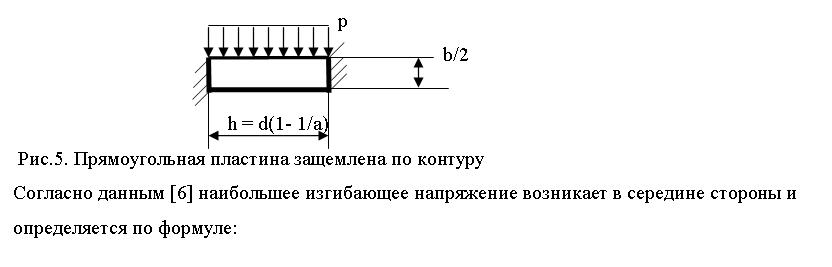
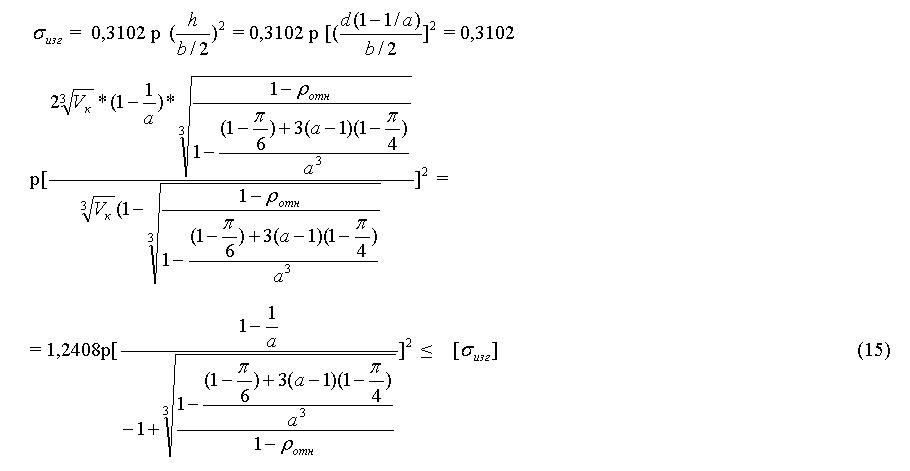
Откуда максимальная удельная нагрузка на ячейку
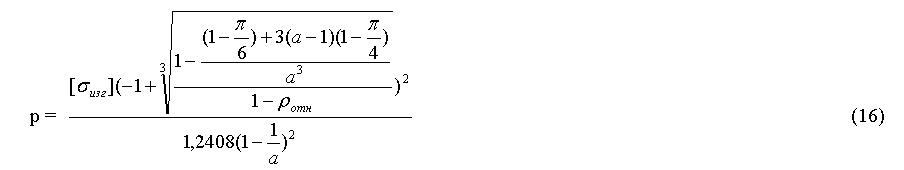
Для хрупких материалов прочность при сжатии значительно выше, чем прочность при изгибе. Коэффициент, представляющий отношение прочности при сжатии к прочности при изгибе КR, составляет:

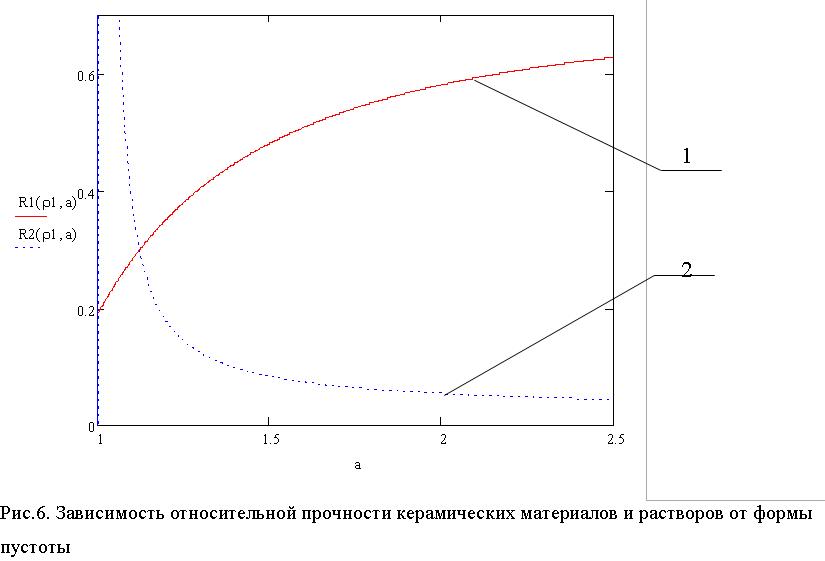
На рис.6 представлена зависимость относительной прочности керамических материалов и растворов от действия сжимающих напряжений (кривая 1) и от действия изгибающих напряжений (кривая 2) при = 0,6 и КR = 5
На рис.7 представлена зависимость относительной прочности гипсовых материалов от действия сжимающих напряжений (кривая 1) и от действия изгибающих напряжений (кривая 2) при = 0,6 и КR = 3
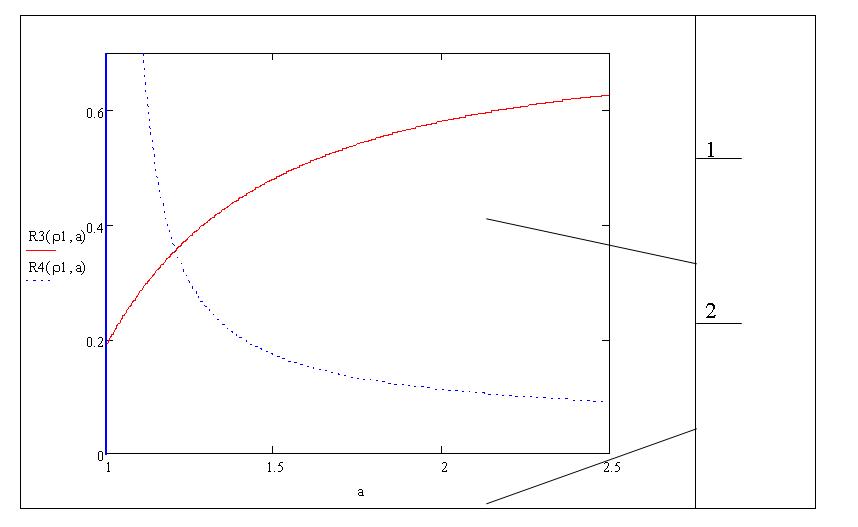
Рис.7. Зависимость относительной прочности гипсовых материалов от формы пустоты
Анализ зависимостей рис.6 и рис.7 показывает, что при шаровой и близкой к ней форме пустоты прочность материала определяется сжимающими напряжениями, а с приближением формы пустоты к кубу (с увеличением коэффициента а) прочность понижается и определяется изгибающими напряжениями.
При а = 2 прочность керамических материалов и растворов понижается в 2,8 раз, а гипсовых материалов в 1, 4 раза.
На рис 8 показана теоретическая зависимость относительной прочности от плотности при различных формах пустоты (а = 1 – шаровые пустоты – кривая 1, а = 2 – кривая 2, а = 5 – кривая 3)
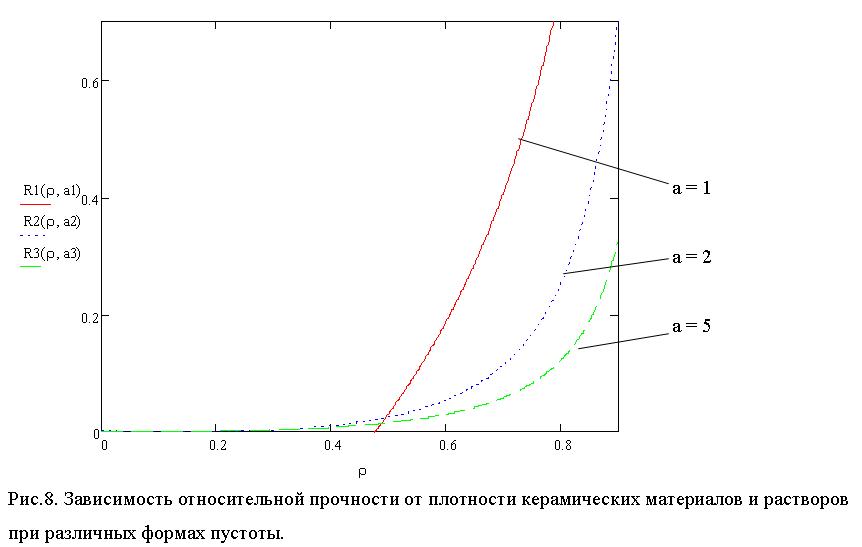
Анализ зависимостей рис.8. показывает, что при относительной плотности материала более 0,5 наибольшая прочность получается при шаровой форме пустоты. Однако, если относительная плотность материала меньше 0,5, то более прочными являются материалы с кубическими пустотами.
Известно [3, стр.92-93], что при резком изменении контура поперечного сечения в местах резкого изменения геометрической формы резко повышается напряжение, т.е. возникает концентрация напряжений. Поэтому для уменьшения концентрации напряжений применяют плавные переходы. В данной работе влияние концентрации напряжений не учитывалось.
Таким образом, при получении материалов с относительной плотностью от 0,1 до 0,4 наиболее рациональной является пустоты в форме многогранника с плавными переходами. Такая структура материала реализуется, например, в пенах.
Для проверки теоретических зависимостей был проведен следующий эксперимент.
Изготовили резиновые пустотообразователи шаровой формы и кубической формы со скругленными гранями (а = 2). Причем объемы и количество пустотообразователей были одинаковы. Данные пустотобразователи были закреплены на тонкие струны в кубической упаковке и помещены в форму размером 100 х 100 х 100 мм. Грани кубических пустотообразователей были расположены параллельно. Формы залили гипсовой смесью одной консистенцией (В/Г = 0,627 для всех образцов). Кроме этого залили форму без пустотообразователей. Образцы после затвердевания вынули из формы и высушили до постоянной массы. Затем определили прочность полученных образцов. Результаты экспериментов представлены в табл.1
Таблица 1.
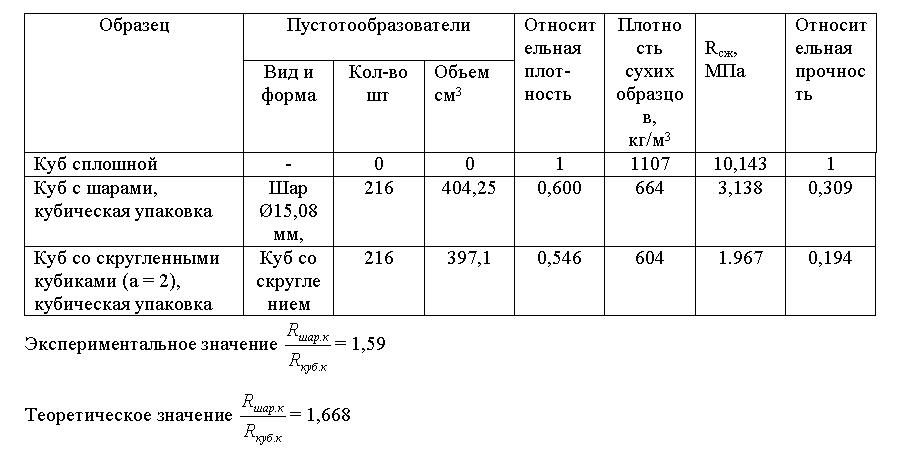
Отклонение теоретического значения от экспериментального составляет 4,6%, что при принятых допущениях является хорошим соответствием.
Для определения влияния хаотичности распределения пустот провели следующий эксперимент: подготовили гипсовую смесь с В/Г = 0,6, смешали с одинаковым количеством (96 штук) шаровых (общий объем 180 см3) и кубических (а = 2, общий объем 177 см3) пустотообразователей и заполнили формы размером 70 х 70 х 70 мм. Образцы после затвердевания вынули из формы и высушили до постоянной массы. Затем определили прочность полученных образцов. Результаты экспериментов представлены в табл.2
Таблица 2
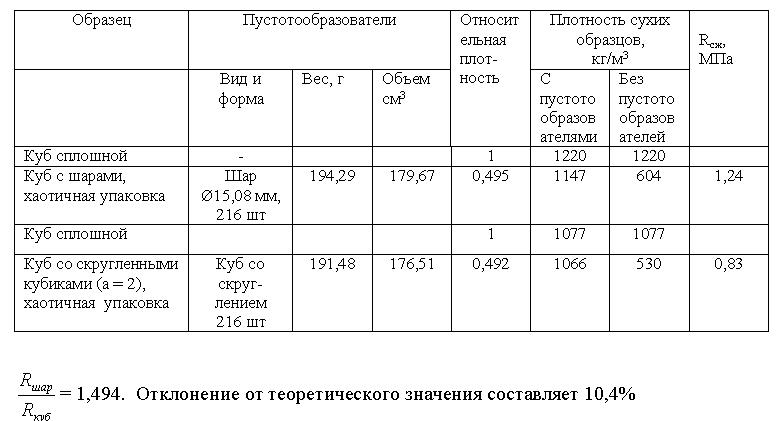
Хаотическое распределения пустотообразователей оказало незначительное влияние на прочность.
Практическое применение результатов теоретических и экспериментальных зависимостей возможно, например, при выборе формы пустот для керамического кирпича. Согласно ГОСТ 530 кирпич керамический выпускается с квадратными и круглыми пустотами (рис.9).
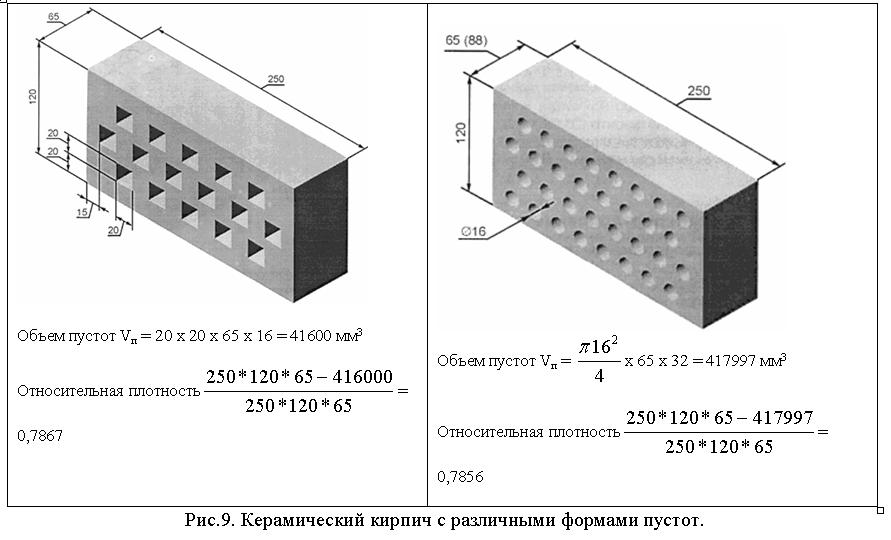
В данном случае при одинаковой относительной плотности предпочтительней использовать кирпич с круглыми отверстиями.
Известно [4], что коэффициент, показывающий долю объема, занимаемого шаровыми пустотами, в зависимости от их расположения составляет:
К1 = 0,52 – при кубической упаковке шаровых пустот;
К1 = 0,729 – при гексагональной упаковке шаровых пустот;
К1 = 0,809 0,812 – при полидисперсном распределении шаровых пустот разного размера;
Таким образом, наиболее рациональной является шаровая форма пустот. Однако, при шаровой форме пустот можно получить минимальную плотность при полидисперсном распределении равную (1-0,812) = 0,188.
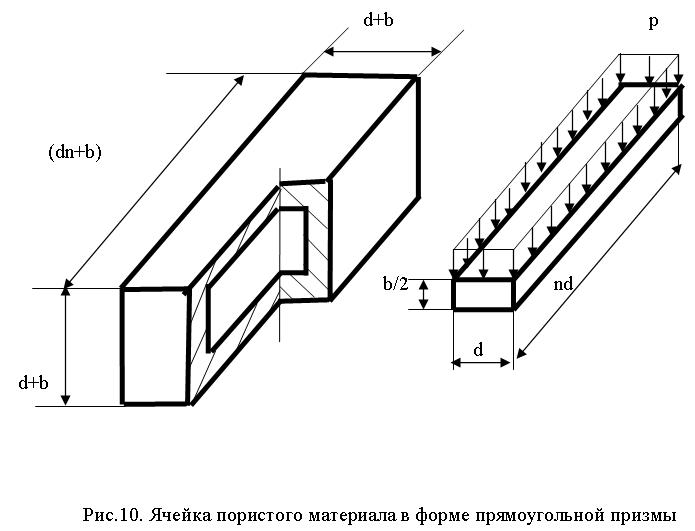
Для определения влияния длины пустотообразователей на прочность рассмотрим ячейку материала (рис.10). Выделим из ячейки элемент размером d x nd x b/2 и рассмотрим его как пластину, защемленную по контуру, и нагруженную распределенной нагрузкой р.

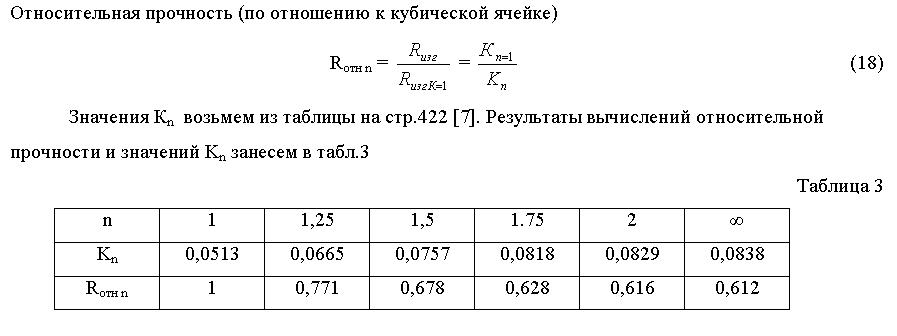
Анализ зависимостей табл.3 показывает, что с увеличением коэффициента «n» (с увеличением отношения наибольшего размера пустоты к наименьшему размеру пустоты) прочность понижается.
В керамической промышленности в качестве порообразователя широко применяются опилки.
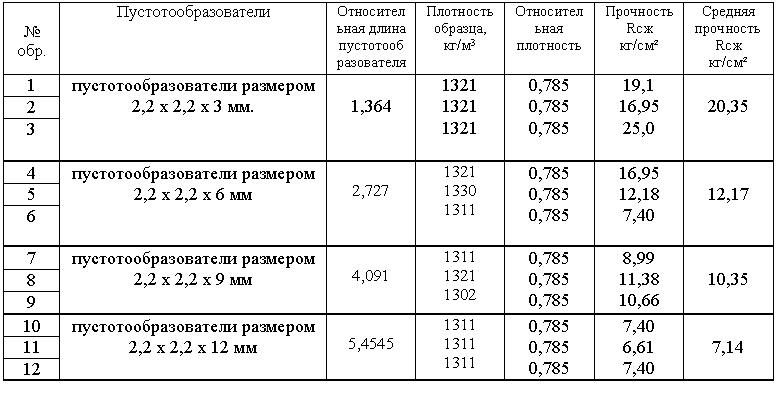
Для определения влияния длины порообразователей (опилок) на прочность керамических изделий проведены экспериментальные исследования глиняных образцов с пустотообразователями в виде скругленных деревянных призм сечением 2,2 х 2,2 мм и длиной 3мм, 6мм, 9мм и 12 мм. Объем пустотообразователей во всех образцах одинаков.
Результаты испытаний представлены в табл.4. Аппроксимируя экспериментальные данные получим зависимость прочности от длины пустотообразователей, на основании которой определили среднюю прочность при n = 1 Rn=1 = 25 кг/см².
Таблица 4
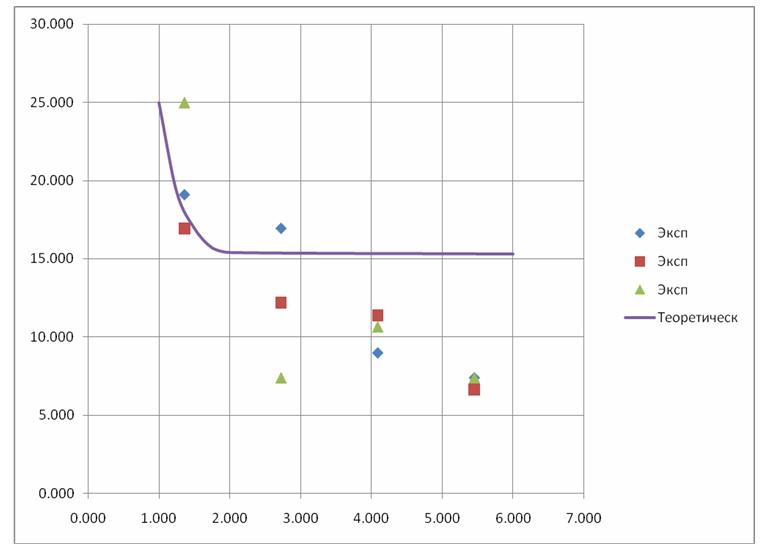
На рис. 9. представлены теоретическая зависимость и экспериментальные данные прочности от длины пустотообразователей.
Анализ данных табл.3, табл.4 и зависимостей рис.9 показывает, что использование коротких опилок при одной и той же плотности материала позволяет увеличить прочность до 2 раз при относительной плотности 0,785. Теоретическая зависимость и экспериментальные данные имеют хорошее совпадение при относительных длинах пустотообразователей от 1 до 3. При увеличении относительной длины пустотообразователей до 5-6 наблюдается значительное расхождение между теоретическими и экспериментальными данными (снижение прочности по теоретическим зависимостям в 1,63 раза, по экспериментальным данным - в 2,8 раза). Это расхождение объясняется, по видимому, тем, что в теоретических зависимостях не учтено влияние степени распределения пустотообразователей с увеличением их длины на прочность материала. С увеличением относительной длины пустотообразователи приобретают свойства фибровых стержней, равномерное распределение которых весьма затруднительно.
R,кг/см2
Относительная длина пустотообразователя, n
Рис. 9. Теоретическая зависимость и экспериментальные данные прочности от длины пустотообразователей.
Выводы:
• структура пустот оказывает существенное влияние на прочность теплоизоляционных силикатных материалов.
• получено теоретическое обоснование и экспериментальные зависимости прочности от формы пустот в теплоизоляционном силикатном материале.
• для повышения прочности пустотелого материала необходимо стремиться к созданию шаровой формы пустот. Переход от кубической формы пустоты к шаровой в зависимости от плотности материала позволяет увеличить прочность в 1,5÷3 раза.
• при получении материалов с относительной плотностью менее (0,188÷0,48) форма пустоты приобретает форму многогранника и необходимо по возможности обеспечить в пустотах плавные переходы.
• при использовании пустотообразователей (опилки, стружки и др.) для повышения прочности материала необходимо стремиться к уменьшению относительной их длины до 1. Использование коротких пустотообразователей позволяет увеличить прочность в 2÷3 раза.
• необходимы дальнейшие исследования по определению влияния формы пустоты и равномерности их распределения при различных плотностях на прочность теплоизоляционных силикатных материалов.
Литература:
1. ПинскерВ.А. "Некоторые вопросы физики ячеистого бетона", Сб. трудов "Жилые дома из ячеистого бетона", Госстройиздат, Ленинградское отделение, с.123 – 143, 1963.
2. Сапелин Н.А. и др. Зависимость прочности бетонов на основе неорганических вяжущих от средней плотности, «Строительные материалы», № 6, 2001 год
3. Степин П.А. Сопротивление материалов. Издание 4-е стереотипное. Издательство «Высшая школа», М. 1968 г, 424 стр.
4. Сапелин Н.А. Влияние геометрических параметров структуры на плотность пористых материалов. Архитектурно-строительное материаловедение на рубеже веков: Материалы международной интернет – конференции. – Белгород: Изд-во БелГТАСМ, 2002, -с.159-166.
5. Липницкий М.Е. Купола (расчет и проектирование). Издательствао литературы по строительству.Л., 1973, 129 стр.
6. Справочник машиностроителя в шести томах. Том 3. Государственное научно-техническое издательство машиностроительной литературы. М, 1955, 564 стр.
7. Феодосьев В.И. Сопротивление материалов. Учебное пособие. Издательство МГТУ им. Н.Э.Баумана, 1999 г, 592 стр.
вернуться в раздел

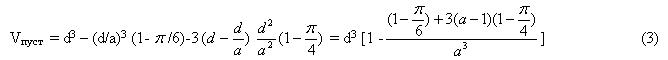
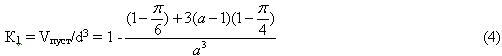

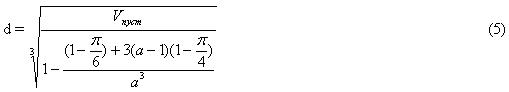
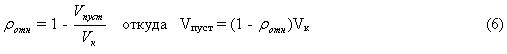
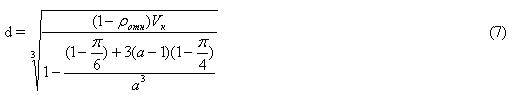
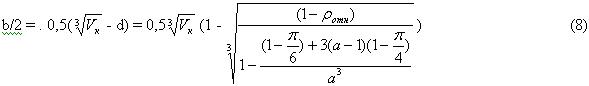
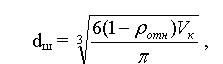
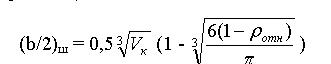 (9)
(9)